Conceptul de continuitate a

Definiția. f (x) funcția. definită într-un cartier al unui. și a numit-o continuă la punctul. dacă (1)

Astfel, funcția f este continua la. în cazul în care sunt îndeplinite următoarele condiții:

1. Funcția f este definită într-un cartier al unui. și anume există un număr astfel încât U;

Funcția de continuitate Determinarea f (x) la. exprimată prin condiția (1) pot fi formulate cu ajutorul (în limbaj) și folosind împrejurimile în termeni de secvențe, respectiv ca

Subliniem că definiția continuității, în contrast cu definiția limitei este considerată completă, și nu înțepat vecinătate a unui punct. și limita funcției este valoarea funcției de la punctul a.

Noi numim x diferența - o creștere a argumentului si se lasa de x. iar diferența f (x) - f (a) - funcția increment. corespunzând unui anumit increment al argumentului x. și lăsați-y. Astfel,

x = x - a, y = f (x) - f (a) = f (a + x) - f (a).

Cu această ecuație notație (1) ia forma

Astfel, continuitatea punctului înseamnă că o creștere infinitezimal a argumentului corespunde unei funcții increment infinitezimal.

Prin analogie cu conceptul de limita stânga (dreapta) a introdus conceptul de continuitate a stânga (dreapta). În cazul în care funcția f este definită pe intervalul și. t.e.f (a - 0) = f (a). atunci această funcție este numită stanga continuă la un.

În mod similar, în cazul în care funcția f este definită pe intervalul și f (a + 0) = f (a). atunci această funcție este numit drept continuă la o.

De exemplu, funcția f (x) = [x] este dreptul continuu până la punctul x = 1 și nu este continuă din partea stângă, în acest moment, deoarece f (1 - 0) = 0, f (1 + 0) = f (1) = 1.

Evident, funcția este continuă în acest moment, dacă și numai dacă este continuă, atât dreapta și la stânga, la acest punct.

La pasul 2, presupunem că funcția definită într-un cartier al unei PUNCTURED.

Un punct este numit un punct de pauză a unei funcții f. în cazul în care această funcție este, fie nu este definit la, sau este definit, dar nu este continuă, la un.

În consecință, și - un punct de discontinuitate a lui f. în cazul în care nu se efectuează cel puțin una dintre următoarele condiții:

2) există un finit

În cazul în care un - un punct de pauză funcția f, iar în acest moment există limite finite la stânga și la dreapta, și anume, punctul este numit un punct de pauză de prim ordin.

continuitate cu o singură față. Puncte de clasificare de discontinuitate.

5.4.1. Determinarea sided continuitate.

Pentru a determina continuitatea funcției la X0 necesită existența și egalitatea. Odată cu aplicarea limitelor unilaterale sunt determinate de conceptul de continuitate a funcției, la stânga și la dreapta:

Opr.5.1.7. f funcție (x) se numește continuă la un punct x0 pe stânga dacă.

Opr.5.1.8. f funcție (x) se numește continuă la dreapta x0 dacă.

Funcția f (x) se numește continuă pe intervalul [a. b], în cazul în care este continuă pe intervalul (a. b), se continuă la dreapta și la stânga continuă la punctul b.

Notă. Functia este continua pe intervalul [a, b] poate fi discontinue la punctele a și b (fig. 1)

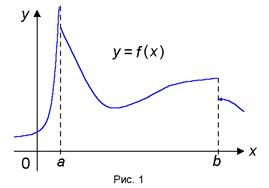
Setul de funcții care sunt continue pe intervalul [a. b] este notat cu C [a. b].

Proprietățile funcțiilor continue pe intervalul

Teorema 1 (v funcție continuă limitată). Dacă funcția f (x) este continua pe intervalul [a. b], este limitată la acest interval, adică există un număr C> 0 astfel încât „x Î [A. b] inegalitatea | f (x) | ≤ C.

Teorema 2 (Weierstrass). Dacă funcția f (x) este continua pe intervalul [a. b], atunci se ajunge la acest segment de valoarea M maximă și valoarea minimă m. și anume există puncte # 945;. # 946; Î [A. b] astfel încât m = f (# 945;) ≤ f (x) ≤ f (# 946;) = M pentru toți x Î [A. b] (Figura 2).

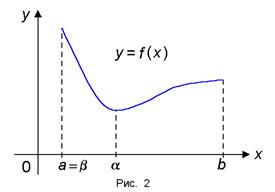
Teorema 3 (existența zero). Dacă funcția f (x) este continua pe intervalul [a. (a. b) b] și la punctele finale ia valori nenule ale diferitelor semne, atunci intervalul există cel puțin un punct # 958; în care f (# 958) = 0.

Sensul geometric al teoremei este că graficul unei funcții care satisface condițiile teoremei, să fie sigur să traverseze axa OX (Figura 3).

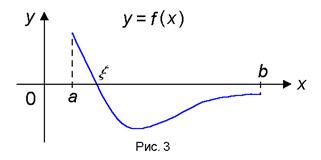
Notă. Pe această metodă bazată pe teorema pentru soluția aproximativă a ecuației