formula barometric
În această secțiune, obținem dependența presiunii gazului \ (P \) pe înălțimea \ (h \) deasupra nivelului mării, în câmpul gravitațional al Pământului.
Să considerăm o coloană de gaz cilindric arbitrar aria secțiunii transversale \ (S \) și o înălțime \ (h. \) Greutate volumul selectat de gaz va fi egal cu \ [F = mg = \ rho Gv = \ rho GHS \] unde \ (\ rho \) densitatea medie a gazului. Densitatea gazului este exprimată prin următoarea formulă: \ [\ necesita P = \ frac = \ frac >>> = \ rho gh. \] Acum ne imaginăm o astfel de coloană în atmosferă și izola în ea o înălțime strat subțire de aer \ (dh \) (Figura \ (1 \)). Este clar că un astfel de strat determină o modificare a presiunii cu o valoare \ [dp = -. \ Rho GDH \] Am stabilit aici semnul minus, deoarece presiunea trebuie să scadă odată cu creșterea altitudinii.
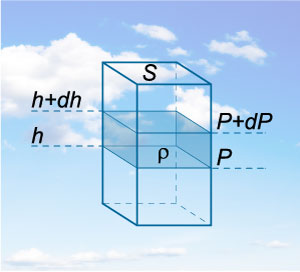
= - \ frac >> dh> \] Ca rezultat, obținem ecuația diferențială care descrie presiunea gazului \ (P \) ca o funcție înălțime \ Rezultatele de integrare în următoarea ecuație: \ [> (h \.).
> = - \ int >> dh>,> \; \; >> h + \ ln C.> \] eliminarea logaritmi, vom găsi așa-numita barometric formula \ [P = C \ exp \ left ( <- \frac>.> H> \ dreapta) \] Constant \ (C \) este determinată din condiția inițială \ (P \ left (\ dreapta) = \) unde \ (\) - este media altitudinea presiunea barometrică.
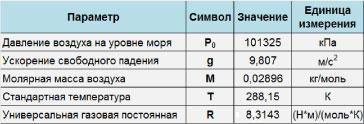
Astfel, dependența presiune atmosferică a înălțimii dat de formula: \ [P = \ exp \ din stânga ( <- \frac>> H> \ dreapta). \] Substituind cunoscute valorile standard, (a se vedea figura \ (2 \) de mai sus), găsim \ (P \ stânga (h \ dreapta) \) (în kilopascali), care este descrisă de formula \ [>> h> \ dreapta)> = \ dreapta) \; \ stânga [\ textul \ dreapta],> \] în cazul în care înălțimea \ (h \) deasupra nivelului mării, exprimată în metri.
Dacă presiunea este determinată în milimetri de mercur \ (\ stânga (\ textul \ dreapta), \) formula barometric devine: \ [P \ stânga (h \ dreapta) = 760 \ exp \ din stânga ( <- 0.00012\,h> \ Dreapta) \ ;. \ stânga [\ textul \ dreapta] \] formula barometrice este utilizat pe scară largă pentru a estima presiunea atmosferică în diferite condiții, chiar dacă dă valori ușor mai ridicate.
Se determină înălțimea la care presiunea aerului este de două ori mai mic decât la nivelul mării?
Pentru a evalua utilizarea formulei înălțimii barometric: \ [P \ stânga (h \ dreapta) = \ exp \ din stânga ( <- 0.00012\,h> \ Dreapta). \] Când \ (h = 0 \) Presiune \ (P \ stânga (h \ dreapta) \) este o presiune medie atmosferică la nivelul mării \ (. \) La o anumită înălțime \ (H \) presiunea va de două ori mai puțin: \ [P \ left (H \ dreapta) = \ frac >> = \ exp \ din stânga ( <- 0.00012\,H> \ Dreapta). \] Rezultă că [\ exp \ din stânga \ ( <- 0.00012\,H> . \ Dreapta) = \ frac \] logaritmare ambelor părți, putem găsi înălțimea \ (H: \) \ [= - 0,00012 \, H,> \; \; \; \; >> \ cca 5780 \, \ textul> \].Găsiți presiunea aerului din mina, la o adâncime \ (1 \, \ textul \) la o temperatură \ (40 \) grade Celsius.
Presiunea aerului din mina poate fi evaluată folosind formula comună barometric. \ [P = \ exp \ din stânga ( <- \frac>.> H> \ dreapta) \] Substituind în această ecuație următoarele valori: \ (h = - 1000 \, \ textul \) (semnul minus corespunde poziției sub nivelul mării), \ (T = 40 + 273.15 = 313.15 \ \ . \ text) cu restul de parametri sunt standard: \ (M = 0.02896 \, \ mare \ frac >> \ normalsize, \) \ (R = 8.3143 \, \ mare \ frac \ cdot \ textul> \ cdot \ textul> \ normalsize , \) \ (g = 9.807 \, \ mare \ frac> ^ 2> \ normalsize. \) După calcule simple ne găsim: \ [> H> \ dreapta)> = \ exp \ stânga [ <- \frac>> \ Stânga ( <- 1000> \ Dreapta)> \ dreapta]> \ aproximativ \ exp \ stânga (\ dreapta)> \ aproximativ> \] Deoarece presiunea atmosferică la nivelul mării este \ (= 760 \ ;. \ text, \) presiunea aerului din arborele va fi egal cu \ (848 \; \ text \), care este de aproximativ \ (12 \% \) peste presiunea standard la nivelul mării.