Funcția continuă 1
Funcția continuă - unul dintre conceptele de bază ale analizei matematice. funcții continue sunt mult mai frecvente decât derivabile. mulțimea tuturor funcțiilor continue este închisă sub operații aritmetice (cu excepția diviziunii), iar compoziția și formele dacă nu cea mai importantă clasă de funcții în analiză. Cu toate acestea, o definiție matematică riguroasă a unei funcții continue, Cauchy deținute - este relativ recentă, și necesită un nivel avansat de abstractizare matematice. Intuitiv aceeași definiție este: o funcție continuă a unei variabile reale, în cazul în care mici modificări în argumentul corespunde mici schimbări în valoare a funcției poate fi scrisă astfel: în cazul în care aceasta înseamnă că graficul funcției continue nu are discontinuități, adică Ea poate fi urmărită „fără a ridica creionul de pe hârtie.“ Toate funcțiile elementare - continuă pe domeniul său.
1. Definiție
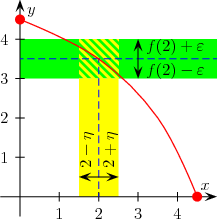
funcție continuă EXEMPLU
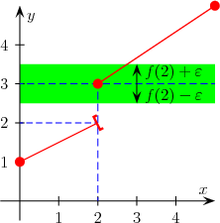
Un exemplu al unei funcții discontinue într-un punct. Funcția nu este continuă din punct de stânga
dar este continuă pe dreapta:
2> f (x) = 3 = f (2) „src = / images / ukbase_1_807531046_1006.jpg />.
Funcția unei variabile reale date în domeniu. Continuu la arbitrar dacă 0 "src = / images / ukbase_1_807536710_299.jpg /> 0, există o" src = / images / ukbase_1_807537385_320.jpg /> (care depinde), care ar trebui să fie o funcție continuă în zonă. În cazul în care se continuă în fiecare punct al acestui domeniu.
Să. - un punct limită de A.
1.1. Definiția continuitate la punctul
Functia f este continuă la un punct în cazul în care:
- funcția f (x) este definit la punctul x 0.
- există o limită
- .
1.2. Definiția de continuitate la punctul de Cauchy
Functia f este continuă la un punct în cazul în care: 0) "src = / images / ukbase_1_807552570_496.jpg /> 0) \ forall x" src = / images / ukbase_1_807553627_612.jpg />. Ce =>
1.3. Definirea continuității la punctul de Heine
Functia f este continuă într-un punct în cazul în care :. În cazul în care. Asta.
2. Inserați puncte
punct de pauză - acesta este un punct (valoarea argumentului), în cazul în care funcția nu este continuă.
Următoarele tipuri de puncte de discontinuitate:
Ruptură numit retractabil, în cazul în care, în acest moment există o funcție limită nu coincide cu funcția de valoare.
Punctul de primul tip este numit un punct de discontinuitate, în cazul în care există granițe stânga și dreapta finite de un anumit punct, iar ei nu se potrivesc.
În cazul în care limita de cel puțin o față nu există, infinit, punctul este numit un punct de pauză de ordinul al doilea.