funcție monotonă
funcție monotonă - o funcție care nu schimbă semnul increment, care este, fie întotdeauna negativ sau întotdeauna pozitiv. În cazul în care, în plus, incrementul nu este zero, atunci funcția se numește strict monotonă. funcție monotonă - o funcție care variază în aceeași direcție.
Funcția este crescută în cazul în care o valoare mai mare a argumentului corespunde unei valori mai mari a funcției. • Funcția scade dacă valoarea mai mare a argumentului corespunde valorii minime a funcției.
condițiile de monotonie:
(Monotonie Criteriul de a avea derivata în intervalul) Fie
continuă pe (a, b), și are la fiecare punct
f derivat „(x). atunci
f crește cu (a, b) dacă și numai dacă
f este în scădere pe (a, b) dacă și numai dacă
O condiție suficientă pentru altă funcție monotonă are un derivat în intervalul) Fie
continuă pe (a, b), și are la fiecare
f derivat „(x). atunci
apoi f strict crescatoare pe (a, b);
atunci f este strict descrescatoare pe intervalul (a, b).
Reciproca nu este adevărat, în general. Derivatul este strict funcție monotonă poate dispărea. Cu toate acestea, setul de puncte în care instrumentul derivat nu este zero, trebuie să fie strâns pe intervalul (a, b). Mai precis deține
(Criteriul de monotonie strict de a avea derivata în intervalul) Fie
și peste tot în derivatul f „(x). Apoi, f strict crescătoare pe intervalul (a, b) dacă și numai dacă următoarele două condiții sunt îndeplinite:
In mod similar, f este în scădere strict intervalul (a, b) dacă și numai dacă următoarele două condiții sunt îndeplinite:
24. Funcții extremelor. O condiție necesară pentru un extremum (teorema lui Fermat). condiția suficientă a extremelor.
O condiție suficientă pentru creșterea funcției (descreștere) asupra intervalului. Conceptul de funcții extreme. O condiție necesară pentru o extremum a funcției (teorema lui Fermat).
Dacă derivatul este o funcție f continuă (x) este pozitiv la un anumit interval (f „(x)> 0), interval, atunci această funcție este în creștere.
Dacă derivatul este o funcție continuă f (x) este negativ la un anumit interval (f „(x)<0), то на этом промежутке функция убывает.
Aceste condiții sunt condiții suficiente pentru creșterea (funcția descreștere).
Vom încerca să înțelegem de ce acest lucru se întâmplă (o dovadă riguroasă este văzută în programul instituțiilor de învățământ superior). Este cunoscut faptul că sensul geometric al derivatului - panta tangentei. Prin urmare, în cazul în care derivatul este pozitiv, unghiul este ascuțit.

Și se pare că programul este „sus pe deal“. În cazul în care derivatul este negativ, unghiul de înclinare este obtuz, se pare că graficul este „în jos“.
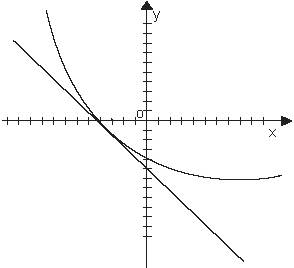
Intervale de creștere și scădere lacunele numite monotonă.
Un punct x0 este un punct al funcției maxime f (x), în cazul în care există un număr pozitiv E, astfel încât pentru orice punct x în intervalul
Cu alte cuvinte, valoarea funcției f (X0) este cea mai mare într-un cartier de X0.
Un punct x0 este un punct de minim al funcției f (x), în cazul în care există un număr E pozitiv, astfel încât pentru orice punct x în intervalul
Cu alte cuvinte, valoarea funcției f (X0) este cea mai mică într-un cartier de X0.
Următorul punct graficul -9 și 3 sunt puncte de maxim și punctul -2 este un punct minim.

Punctul de puncte maxime sau minime sunt numite extreme.
Teorema lui Fermat: Dacă x0 - funcție continuă punctul extremum f (x), atunci f „(x0) = 0.
Geometric, se pare ca acest lucru: la extremum tangenta paralel cu axa OX și, prin urmare, unghiul de înclinare este 0.

Această condiție este necesară, dar nu suficientă, pentru un extremum.