funcții monotone

Determinarea creșterii și funcție descrescătoare

Să \ (y = f \ stânga (x \ dreapta) \) este o funcție diferențiabilă a intervalului \ (\ stânga (\ dreapta). \) Funcția se numește creștere (sau non-descreștere), la un anumit interval de timp, dacă pentru orice puncte \ (\ în \ stânga (\ dreapta), \) astfel încât \ (0, \) astfel încât \ [\ forall \; x \ în \ stânga (- \ delta,> \ dreapta) \ rightarrow f \ stânga (x \ dreapta), f \ stânga (> \ dreapta). \] in mod similar determinate strict scăderea funcției \ (y = f \ stânga (x \ dreapta) \) la punctul \ (. \)

Criteriul de creștere și funcție descrescătoare

Luați în considerare din nou funcția \ (y = f \ stânga (x \ dreapta), \) presupunând diferențiabilă său într-un interval \ (\ stânga (\ dreapta). \) Creșterea sau descreșterea funcției pe intervalul este determinat de semnul prima funcție derivată.

Teorema 1.
Pentru a funcționa \ (y = f \ stânga (x \ dreapta) \) a crescut în intervalul \ (\ stânga (\ dreapta), \), este necesar și suficient ca prima derivată a funcției a fost un non-negativ pretutindeni în acest interval de: \ [f „\ stânga (x \ dreapta) \ ge 0 \; \ forall \; x \ în \ stânga (\ dreapta) \.] acelaşi criteriu este valabil pentru cazul funcției, reducerea intervalului \ (\ stânga (\ dreapta): \) \ [f „\ stânga (x \ dreapta) \ le 0 \; \ forall \ ;. x \ în \ stânga (\ dreapta) \] Vom demonstra teorema ambelor părți (necesare și suficiente) pentru cazul unei funcții de creștere.

O condiție necesară.
Să considerăm un punct \ arbitrar (\ în \ stânga (\ dreapta). \) Dacă (= f \ la stânga y (x \ dreapta) \) funcția \ crește prin \ (\ stânga (\ dreapta), \), atunci, prin definiție poate fi scrisă că \ [\ forall \; x \ în \ stânga (\ dreapta): x> \ rightarrow f \ stânga (x \ dreapta)> f \ stânga (> \ dreapta); \] \ [\ forall \; x \ în \ stânga (\ dreapta): x 0 \) peste tot în intervalul \ (\ stânga (\ dreapta), \), cu excepția poate doar câteva puncte selectate la care \ (f „\ stânga (x \ dreapta) = 0, \ ) atunci funcția \ (f \ stânga (x \ dreapta) \) este strict în creștere.

Prin urmare, condiția \ (f „\ stânga (x \ dreapta) 0 \), atunci funcția \ (f \ stânga (x \ dreapta) \) strict în creștere, la punctul \ (\);

Dacă \ (f „\ stânga (> \ dreapta) 0 \) și \ (+ >> 0 \) (ca valori non-negative, \ (x \), sunt luate în considerare cu condiția). Rezultatul este: \ [-> \ dreapta) \ stânga (+> \ dreapta)> 0,> \; \;> \ dreapta) - f \ stânga (> \ dreapta)> 0.> \] Aceasta înseamnă pentru a determina că funcția \ (f \ stânga (x \ dreapta) = + 1 \) este un strict crescătoare la un interval predeterminat.

Toate valorile \ (o \), pentru care ecuația \ (- 6 + 9x + a = 0 \) are trei rădăcini reale distincte.

O funcție cub este definit și derivabile pe linia reală întreg. derivatul său este dat de \ [- 6 + 9x + a> \ dreapta) ^ \ prime >> = - 12x + 9.> \] Prin echivalarea derivatului la zero, vom defini funcția intervale monotonie (Figura \ (15 \)): \ [\ ; \; - 12x + 9 = 0> \; \; - 4x + 3 = 0,> \; \; = 1 \; = 3> \]

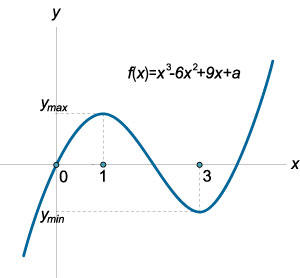
Deci, trecerea (de la stânga la dreapta), prin punctul \ (x = 1 \) creșterea funcției este înlocuită cu scăderea acesteia, și anume \ (X = 1 \) este punctul funcției maxime. In mod similar, \ (x = 3 \) este punctul minim al funcției. Ecuația cubi va avea trei rădăcini reale distincte în cazul prezentat în figură \ (16 \). Funcția maximă trebuie să aibă o valoare pozitivă, iar cea minimă - este negativ. Astfel, se ajunge la următoarea condiție: \ [\ left \<\begin y\left( 1 \right)> 0 \\ y \ stânga (3 \ dreapta) 0 \\ y \ stânga (3 \ dreapta) 0 \\ a - 4 \\ a 0. \) Rezolvarea acestei inegalități, obținem: \ [> \ cdot >> 0, > \; \; \ Dreapta) \ stânga (\ dreapta)> 0,> \; \; -> 0,> \; \; >> \; \; 16.> \]