funcţia de continuitate

Conceptul de matematică funcție continuă veni, în primul rând studierea diferitelor legi ale mișcării. Timpul și spațiul sunt infinite, și dependența, de exemplu, calea de e momentul t. legea exprimată s = f (t). Acesta oferă un exemplu al unei funcții f continue (t). Modificări continuu, iar temperatura apei încălzite, este de asemenea o funcție continuă de timp: T = f (t). linie continuă și, în cazul în care poate fi trasă fără a ridica creionul de pe hârtie. Această linie este graficul unei funcții continue.

Grafic funcția este continuă la un punct în cazul în care graficul acesteia nu este „spart“ în acest moment. Grafic o funcție continuă - este prezentată mai jos.

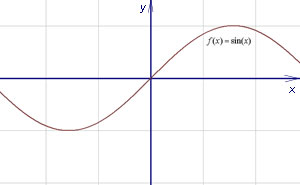
Funcția de continuitate Determinarea prin limită. Funcția este continuă în punctul supus trei condiții:

1. Funcția definită în punctul.

2. Există o funcție limită într-un punct, la dreapta și la stânga limite sunt egale.

3. Funcția limită la un punct egală cu valoarea funcției în acest moment:

În cazul în care nu este îndeplinită cel puțin una dintre aceste condiții, funcția nu este continuă în punctul. În același timp, se spune că funcția este discontinuă, iar punctele de pe grafic în care programul este întrerupt, numite puncte de discontinuitate. Graficul unei astfel de funcții, pâraie discontinuitatea la x = 2 - de mai jos.

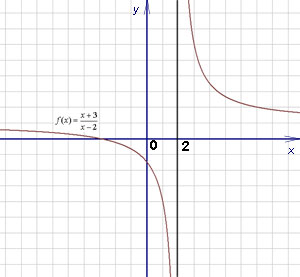
Exemplul 1. f funcție (x) este definit după cum urmează:

Dacă această funcție este continuă în fiecare dintre punctele de frontieră ale ramurilor sale, adică, la punctele x = 0. x = 1 x = 3?

Decizie. Verificăm toate cele trei condiții de continuitate a funcției de la fiecare punct de delimitare. Prima condiție este îndeplinită, din moment ce această funcție este definită în fiecare dintre punctele de frontieră, rezultă din definiția funcției. Rămâne să verifice celelalte două condiții.

Punctul x = 0. Am găsit o limită la stânga la acest punct:

Găsiți o limită dreapta:

Funcția limită și valoarea funcției în punctul x = 0 trebuie să se regăsească în ramurile funcției, care include acest punct, adică a doua ramură. Găsiți-le:

După cum se poate observa, iar valoarea limită fuktsii a funcției x = 0 sunt egale. Prin urmare, funcția este continuă la x = 0.

Punctul x = 1. Constatăm limita stanga la acest punct:

Găsiți o limită dreapta:

Funcția limită și valoarea funcției în punctul x = 1 trebuie să se regăsească în ramurile funcției, care include acest punct, adică a doua ramură. Găsiți-le:

Limita Fuktsii și valoarea funcției x = 1 este egal. Prin urmare, funcția este continuă la x = 1.

Punctul x = 3. Să ne găsim o limită la stânga la acest punct:

Găsiți o limită dreapta:

Funcția limită și valoarea funcției în punctul x = 3 se găsesc în ramurile funcției, care include acest punct, adică a doua ramură. Găsiți-le:

Limita Fuktsii și valoarea funcției x = 3 sunt egale. Prin urmare, funcția este continuă la x = 3.

Astfel, această funcție este continuă în fiecare punct limită.

schimbarea continuă a funcției poate fi definită ca schimbarea treptată, fără salturi, în cazul în care o mică schimbare mică schimbare atrage după sine funcția de argument.

Să ilustrăm această schimbare continuă a funcției ca un exemplu.

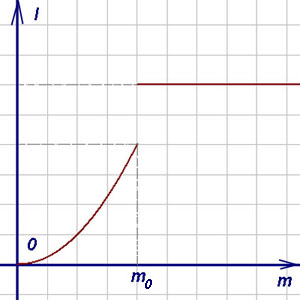
Să mai sus atârnă de masă de o sarcină fir. Sub efectul acestui fir de sarcină este întinsă, astfel încât distanța L din punctul fire de suspensie de sarcină este o funcție de masa m sarcină. adică l = f (m). m ≥0.

Dacă modificați o masă puțin a mărfurilor, distanța L schimbă puțin. Astfel, mici modificări ale m corespund mici schimbări l. Cu toate acestea, în cazul în care greutatea sarcinii este aproape de rezistența maximă a firului, o mică creștere în masa sarcinii poate cauza de rupere a firului: brusc distanța l crește și devine egală cu distanța de la punctul de suspensie la suprafața mesei. Graful l = f (m) este prezentată în Fig. Pe teren acest grafic este continuă linia (solid), iar la punctul în care a fost suspendat. Rezultatul este un grafic care constă din cele două ramuri. Toate punctele cu excepția funcției l = f (m) este continuă și are la ruptura punct.

Investigarea continuității poate fi ca o sarcină independentă, și una dintre etapele unei investigații complete a funcției și construirea programului său.

Continuitatea diferenței. Lăsați funcția y = f (x) definit pe intervalul] a. b [și continuă în fiecare punct al intervalului. Apoi se spune să fie continuu în intervalul] a. b [. În mod similar, conceptul de continuitate se determină intervalele de forma] - ∞, b [. ] A. + ∞ [. ] - ∞, + ∞ [. Să presupunem acum că funcția y = f (x) definită pe intervalul [a. b]. Diferența dintre intervalul și intervalul: puncte limită interval nu sunt incluse în intervalul, iar punctele limită ale intervalului sunt incluse în segmentul. Aici ar trebui să menționăm așa-numita continuitatea unilaterală: punctul A. rămânând pe intervalul [a. b]. putem aborda numai dreptul și la punctul b - doar la stânga. Funcția se numește continuă pe intervalul [a. b]. în cazul în care este continuă la toate punctele interioare ale acestui segment este continuă la dreapta și la stânga un continuu la punctul b.

Un exemplu al unei funcții continue poate fi oricare dintre funcțiile elementare. Fiecare funcție elementară este continuă la orice interval în care este definit. De exemplu, funcțiile sunt continue și la orice interval [a. b]. este continua pe intervalul [0. b]. este continuu la orice interval care nu conține punctul a = 2.

Exemplul 2. Pentru a investiga functia de continuitate.

Decizie. Noi verificam prima condiție. Funcția nu este definit la punctele - 3 și nu se realizează 3. Cel puțin una dintre condițiile de continuitate a liniei reale întreg. Prin urmare, această funcție este continuă la intervale

Exemplul 3. Pentru a determina la ce valoare a parametrului de-a lungul unei funcții de domeniu continuu

Decizie.
Am găsit o funcție limită stânga la:

Am găsit limita din dreapta atunci când:

Evident, valoarea în punctul x = 2 ar trebui să fie egală cu ax: