funcţia Onnost

funcție monotonă - o funcție care nu schimbă semnul increment, care este întotdeauna un non-negativ sau non-pozitive întotdeauna. În cazul în care, în plus, incrementul nu este zero, atunci funcția se numește strict monotonă. funcție monotonă - o funcție care variază în aceeași direcție.

Funcția este crescută în cazul în care o valoare mai mare a argumentului corespunde unei valori mai mari a funcției. Funcția scade dacă valoarea mai mare a argumentului corespunde valorii minime a funcției.

Să o funcție de timp

Funcția este declarat a fi în creștere pe dacă

.

Funcția se numește strict în creștere pe dacă

.

Funcția este numit în scădere, dacă pe

.

Funcția se numește strict descrescătoare pe dacă

.

(Strict) creșterea sau scăderea funcției se numește (strict) monotonă.

Funcția y = f (x) se numește creștere (descreștere) un anumit interval de timp, în cazul în care x1 f (x2)).

Dacă funcția diferențiabilă y = f (x) în intervalul [a, b] crește (scade), derivatul pe acest interval f „(x)> 0

punctul Ho se numește un maxim local (minim) al funcției f (x), în cazul în care există o vecinătate Ho, pentru toate punctele în care inegalitatea f (x) ≤ f (Ho) (f (x) ≥ f (Ho)).

Punctul maxim și minim extremelor sunt numite puncte, iar valorile funcției la aceste puncte - extremele ei.

Condițiile necesare pentru un extremum. Dacă Ho este un extremum punct al funcției f (x), atunci fie f „(Ho) = 0 sau f (Ho) nu există. Aceste puncte sunt numite critice, iar funcția este determinată la punctul critic. Extremele funcții se găsesc printre punctele sale critice.

Prima condiție este suficientă. Să Ho - un punct critic. Dacă f „(x) atunci când trece prin punctul Ho schimbă semnul de la plus la minus, apoi la punctul de funcția Ho are un maxim, în caz contrar - cel puțin. Dacă trec prin punctul critic al derivatului nu se schimbă semnul, apoi la punctul Ho nu este extremelor.

A doua condiție suficientă. Să presupunem că funcția f (x) este f derivat „(x) într-un cartier al Ho și al doilea derivat de la punctul Ho. Dacă f „(Ho) = 0,> 0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

Pe intervalul [a, b] funcția y = f (x) poate ajunge la cea mai mică sau cea mai mare valoare sau punctele critice sau segmentele de la capete [a, b].

convexitate 7.Intervaly, concavitate de topire inflexiune.

Graful y = f (x) este declarat a fi convex în intervalul (a, b). dacă este poziționat mai mică decât oricare dintre tangenta sale în acest interval.

Graful y = f (x) se numește concavă pe intervalul (a, b). în cazul în care este în oricare dintre tangenta în acest interval.

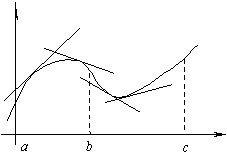
Figura arată curba, convexă pe (a, b) și concavă (b; c).

convex semicercul pe [-1; 1].

Parabolei y = x2 concavă pe intervalul (-∞; + ∞).

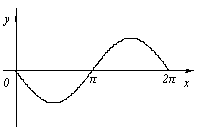
Funcția Program în aceleași intervale pot fi convexe și concave cealaltă. Deoarece graficul y = sin x la [0,2; π], convexe în intervalul (0; π) și concave (π; 2π).

Să considerăm un criteriu suficient care permite să se determine dacă graficul funcției este în intervalul de convexe sau concave.

Teorema. Să presupunem că y = f (x) este derivabila (a, b). În cazul în care toate punctele intervalului (a; b) derivata a doua a funcției y = f (x) este negativă, adică, f '' (x) <0, то график функции на этом интервале выпуклый, если же f ''(x )> 0 - concave.

Dovada. Presupunem pentru definiteness că f '' (x) <0 и докажем, что график функции будет выпуклым.

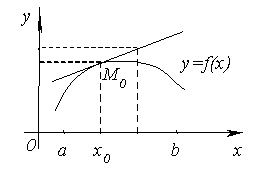
Să considerăm funcția graficului y = f (x) punct arbitrar cu abscisa M0 x0  (a, b) și trage o tangentă prin punctul M0. ecuația lui. Vom arăta că graficul funcției (a, b) este sub această tangentă, adică la una și aceeași valoare x ordonata curbei y = f (x) este mai mică decât tangenta ordonată.

punctul de inflexiune funcția

În acest termen, există alte utilizări, vezi. Punctul de inflexiune.

Inflexiei punct funcție de determinare a tochkaoblasti interioare astfel chtonepreryvna în acest moment, există un derivat determinat caracterul finit sau infinit în acest punct, atât final iyavlyaetsya convexitate strict al intervalului și de pornire convexitatea strict interval în jos, sau invers.

În acest caz, punctul de inflexiune yavlyaetsyatochkoy a graficului funcției, adică, graficul funcției la „înclină“ cherezkasatelnuyu să-l în acest moment: atunci când este tangenta sub grafic, și deasupra graficului pri- (sau invers)

O condiție necesară pentru existența unui punct de inflexiune, dacă funcția f (x), de două ori diferențiabilă într-un cartier al punctului de inflexiune a vtochku atunci.

O condiție suficientă este existența unui punct de inflexiune, dacă funcția într-un cartier tochkiraz continuu diferențiabilă și prichemnechotno, și în care, o, funktsiyaimeet vtochku inflexiune.