funcţii de interpolare
Principalele aspecte abordate în curs:
1. Concepte de bază de interpolare, problema care duce la apropierea funcțiilor, sensul geometric al interpolare
2. Lagrange de interpolare polinomiale
3. Schema Aitken
4. O estimare eroare Lagrange formula de interpolare
5. diferențe finite
6. Newton formula interpolare
§ primă formulă de interpolare Newton
§ a doua formulă de interpolare Newton
7. Evaluarea prima și a doua erori Newton formula interpolare
8. interpolare inversă
9. interpolare Spline
- Concepte de bază ale problemelor de interpolare care conduc la funcția de aproximare
Interpolarea (din interpolarea latină -. Variation, modificare) - matematică și statistică, determinarea valorii valorilor intermediare pentru unele cunoscute valorile sale [SAA. Dicționarul Enciclopedic].
Probleme care duc la apropierea funcțiilor este după cum urmează. Valori cunoscute ale funcției f (x) la punctele x1. x2. xn; aveți nevoie pentru a recupera valoarea sa în alte lui.
Interpolarea proprietățile de transmitere polinomiale ale funcției f (x) va fi construit sub forma:
Pn (x) = c1 # 966; 1 (x) + c2 # 966; 2 (x) +. + cn # 966; n (x), unde # 966; 1 (x), # 966; 2 (x). # 966; n (x) - o clasă de funcții liniar independente, în care Pn (xi) = f (xi), i = 1, 2. n.
Astfel, Pn (x) f (x).
Punctul x1. x2. xn se numesc puncte de interpolare.
· Lagrange de interpolare polinomiale
Să presupunem că valoarea funcției f (x) în (n + 1), punctul x0. x1. xn. Apoi polinomul Lagrange proprietăți ale funcției f (x) transmiterea, poate fi scrisă ca:
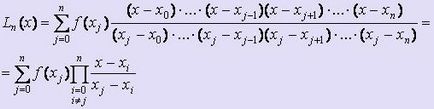
schema Aitken oferă o formă mai convenabilă de a găsi polinomul Lagrange.
Ideea de bază a acestei metode este după cum urmează.
În prima etapă se calculează L0,1 polinoame (x), L1,2 (x). Ln-1, n (x), construită pe fiecare pereche de noduri adiacente 0,1; 1.2; :; n-1, n respectiv.
În același timp. . .
Astfel, polinoamele sunt construite pe două noduri adiacente sunt calculate în conformitate cu formulele.
Apoi, pe baza acestor polinoame sunt calculate polinoame construite la tripletele nodurilor adiacente :.
Etc. până când veți obține un polinom construit pe toate nodurile de interpolare :.
Rezultat polinomială L0, 1. n (x) Ln (x).
· Estimarea erorilor de interpolare Lagrange formula
Avem yj = f (xj), Ln (x). Ln (x) polinomul este construit astfel încât Ln (xj) = f (xj).
Calculând eroarea Rn (x), astfel: Rn (x) = f (x) - Ln (x). Puteți obține următoarea formulă pentru eroarea de estimare a Lagrange formula de interpolare:
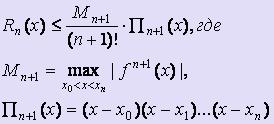
O astfel de evaluare este posibilă numai atunci când știi expresia analitică pentru f. Dacă f este definit în formă de tabel, derivații sunt înlocuite cu diferențe finite.
· Newton formula interpolare
1. Gradul de polinomului nu depășește n.
Formula Pn (x) pentru prima formulă de interpolare Newton este după cum urmează :.
unde q = (x - x0) / h.
Prima formulă de interpolare a lui Newton este utilizată dacă x este începutul mesei. Apoi, după cum X0 ar trebui să fie luate în curând lăsat la o anumită x valoarea tabelară.
- A doua formulă de interpolare Newton
Atunci când o valoare argument este mai aproape de sfârșitul intervalului de interpolare, se aplică o primă formulă de interpolare devine neprofitabilă.
În acest scop, a doua Newton de interpolare formula.
unde q = (x - xn) / h.
Aici, după cum xn ar trebui să ia imediat dreptul la un anumit x valoarea tabelară.
· Evaluarea erorilor de prima și a doua formulă de interpolare Newton
Folosind substituirea q = (x - x0) / h și q = (x - xn) / h și înlocuind în mod adecvat de expresie Pn + 1 (x) în eroare formula estimarea formulei de interpolare Lagrange, obținem o formulă pentru estimarea erorii de interpolare pentru primul și a doua formulă de interpolare Newton, respectiv:
.
.
Problema interpolării inverse este după cum urmează. Dacă yi valorile> din tabel sunt în ordine crescătoare sau descrescătoare, funcția y = f (x) este monotonă în [x0. xn], iar aceeași masă poate fi interpretată ca stabilind un mod discret o funcție x = # 966; (y). inversul funcției y = f (x). Pentru această funcție de feedback poate fi, de asemenea, sarcina de interpolare: găsirea unei valori x * cu o valoare predeterminată y *.
Să xi> nodurile echidistante situate la o distanță h față de altul și construite de una dintre polinoame Newton (pentru certitudine - prima).
La soluționarea problemei inverse a interpolare folosind acest polinomiale, în partea stângă este valoarea cunoscută a lui y *. iar formula în sine devine o ecuație algebrică în raport cu x. Dacă numerele yi> în ordine crescătoare sau descrescătoare, această ecuație are o soluție unică pe [x0. xn].
Decizia sa trebuie să fie solicitată de către oricare dintre metodele studiate anterior pentru rezolvarea ecuațiilor neliniare.
În cazul nostru, modul cel mai natural de a rezolva ecuatia este simpla repetare.
Înlocuim y = y * în formula de mai sus și de a converti ecuația rezultată a formei.
Această ecuație are structura = x # 966; (x). și anume de tip adecvat pentru aplicarea metodei de iterare simple.
Ca o aproximare inițială putem lua valoarea x (0) = xi. aproape de * x dorită. Cu aproximație x inițială (0). Construim un proces iterativ pentru rezolvarea ecuației rezultată până când se atinge precizia specificată:
Cu un număr mare de puncte de interpolare puternic grad polinoame interpolate crește, ceea ce le face incomod pentru calcule.
În acest caz, este convenabil de a folosi un tip special de interpolare polinomiale porțiuni - spline de interpolare.
Esența acestei abordări este după cum urmează.
Definiția. Lăsați intervalul [a, b] este împărțit în n puncte de segmente parțiale [xi. xi + 1], i = 0, 1. n-1. Funcția spline M-comandă se numește Sm (x). cu următoarele proprietăți:
1) Funcția Sm (x) este continua pe intervalul [a, b], împreună cu derivații acestora până la un anumit ordin p.
2) La fiecare interval [xi. xi + 1] Funcția coincide cu unele mnogochlenomPm algebric, i (x) de grad m.
Diferența de m - p între gradul de cel mai înalt ordin al spline și continue pe intervalul [a, b] se numește derivatul spline defect.
Considerăm spline, un defect care este 1.
Cele mai utilizate pe scară largă cubi spline S3 (x).
Astfel, pentru interpolarea spline necesară pentru a construi astfel încât S (xi) = yi. i = 0, 1. n.
Prin definiție, spline poate fi scris ca:
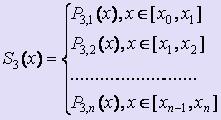
în care fiecare dintre P 3, i (x) - al treilea grad :. polinom
Coeficienții ai = yi.
Se poate demonstra că coeficienții ci sunt calculate prin formula :.
Pentru a calcula di coeficienți sunt folosiți formula.
Pentru a calcula bi coeficienți - formulă.