legile matematicii
În viața noastră, există legi care trebuie respectate. Respectarea legilor garantează stabilitatea și dezvoltarea armonioasă. Nerespectarea legilor conduce la consecințe triste.
În matematică are propriile sale legi, care trebuie să fie, de asemenea, respectate. Nerespectarea legilor matematicii, cel mai bun caz, să conducă la faptul că scorul elevului este redusă, iar în cel mai rău caz (care este răspândit mai puțin) conduce la faptul că planul de incident, atarna calculatoare peste acoperișurile se îndepărteze de vânt puternic, calitatea comunicării se deteriorează, cineva foame, și cineva zhiruet etc.
Legile constau proprietăți matematice simple. Aceste proprietăți, s-ar putea fi deja familiare. Dar nu ezita sa le amintesc din nou, și este cel mai bine să scrie sau să memoreze.
Comutativitate de adăugare
Aceasta este prima lege a matematicii. El spune că permutarea termenilor de scaune, suma nu se schimba. Nimic nou. Într-adevăr, se adaugă cinci-doi, pentru a primi sapte. Pe de altă parte, adaugă la egalitate de puncte cu cinci, pentru a primi sapte din nou:
Dacă ne-am pus pe o scară de 10 kg de mere și celălalt bol și a pus 10 kilograme de mere, apoi aliniați scara, și nu contează că merele din pachetele sunt la întâmplare. Dacă luăm pachetul cu echilibrul si se amesteca merele sunt acolo, cum ar fi bile de loterie în sac, pachet de tot ceea ce va cântări, de asemenea, 10 kg. Prin transpunerea sumă nu este schimbat. Termenii în acest caz, merele, iar suma este greutatea finală.
Astfel, printre expresiile 2 și 5 2 + 5 poate echivala. Acest lucru va însemna că suma lor este egală cu.
Noi credem că am învățat una din lecțiile anterioare, numite „expresie“, asa ca am unabashedly scrie proprietatea comutativă de adiție folosind variabile:
Comutativitate înregistrate de adăugare va lucra pentru orice numere. De exemplu, să ia oricare două numere lasa un = 2, b = 3. Am alocat variabile a și b sunt valorile 2 și 3, respectiv. Acum, ei merg la expresia principală a + b = b + a și înlocuind acolo unde este necesar. substitutiv deuce „un“ triplu substitut „b“
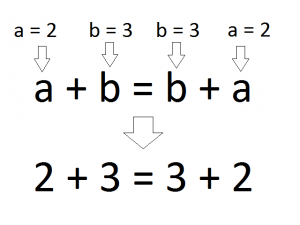
Ca urmare, avem:
Comutativitate de multiplicare
Comutativitate de multiplicare - a doua lege. El spune că, dacă deînmulțitul și multiplicatorul sunt interschimbate, atunci produsul nu se va schimba. Să verifice dacă acest lucru este așa. Înmulțiți cu cinci până la egalitate de puncte, egalitate de puncte și apoi vice-versa la cinci.
Da, produsul nu se schimbă. lucrări de drept. În matematică este bună - nu există nici o minciună, fără excepții, fără corupție. De cinci ori doi este de zece, și două înmulțit cu cinci-zece prea. Și nimic altceva.
Scriem proprietatea comutativă de multiplicare folosind variabile:
De altfel, proprietățile de înregistrare și legi ca variabile este utilizată în mod opțional literele a și b. Puteți folosi orice alte caractere, cum ar fi c și d sau x și y. De exemplu, aceeași proprietate poate fi scris ca:
Care sunt literele folosite ca variabile pentru tine de a decide.
asociativitate de adăugare
Proprietatea asociativ de plus este legea care spune că rezultatul adăugării mai multor termeni nu depind de ordinea de acțiune. În plus, legea vă permite termeni de grup pentru comoditate de calcul (și pentru frumusețe, de asemenea). De exemplu, se adaugă cele trei termeni:
Toți termenii de această expresie este adăugată (conectată prin semnul +), ceea ce înseamnă că puteți utiliza legea asociativă de adăugare, adică, termeni pot fi grupate. Grupul poate fi orice doriți - acest rezultat nu se va schimba. Luați în considerare două tipuri de grupuri:
Astfel, printre expresiile (2 + 3) + 5 și 2 + (3 + 5) poate echivala cauza lor general același rezultat.
Scriem proprietatea asociativă folosind variabile:
(A + b) + c = a + (b + c)
proprietate distributivă de multiplicare
distributivitate de multiplicare permite de a se multiplica suma cu numărul. Cuvântul „distribuitor“ vorbește de la sine - pentru a distribui.
Să considerăm un exemplu. Să presupunem că înainte de a ne este de a găsi valoarea următoarea expresie:
Știm că trebuie mai întâi să efectueze o acțiune între paranteze. Realizăm:
Acum vom schimba bracket nostru a primit opt:
Am primit un răspuns 16. Același exemplu poate fi rezolvată folosind proprietatea distributiv de multiplicare. În acest scop, fiecare termen care, în paranteze înmulțit cu 2, și se adaugă în sus rezultatele:
Ambele metode dau același răspuns. A doua metodă, pe care am considerat - aceasta este proprietatea distributiv de multiplicare. Odată ce am considerat că este foarte detaliat și a dislocat. La școală, acest exemplu ar fi înregistrate în foarte scurt timp. Pentru acest record, de asemenea, trebuie să se obișnuiască. Se pare ca acest lucru:
(3 + 5) x 2 = 2 + 3 x 5 x = 6 + 2 10 = 16
Acum vom scrie proprietatea distributiv de multiplicare folosind variabile:
(A + b) x c = a × c + b × c
La această oprire. Există și alte legi ale matematicii, dar am până acum nu vor fi luate în considerare. La început luate în considerare în această lecție va fi de ajuns.
La fel ca lecția?
Alăturați-vă noul nostru grup Vkontakte și începe să primească notificări despre noi lecții
Aș adăuga numele legii - distributiva, comutativă, asociativă. În fizică și matematică shuolah dau aceste nume. Îmi place ideea proiectului - nu se ajustează la manualele și programele. Să vă rugăm informațiile cele mai complete, redundante. De asemenea, uneori, pe care doriți să citiți povești interesante. Cine a inventat, așa cum a făcut înainte? Deoarece înregistrarea sa schimbat în timp?
Foarte ușor de înțeles și ușor sunt explicate! Site-ul este super! Tine-te de lucru bun! tu și toate cele bune mulțumesc.
Aceasta poate ajuta la Ege?
Vă mulțumesc foarte mult pentru site-ul, vă rugăm să nu se opresc aici, vă doresc fericire și succes în toate eforturile dumneavoastră.