Calculator on-line - decizie ecuații logaritmice

Acest calculator matematic online pentru a vă ajuta să rezolve o ecuație logaritmică. Program pentru rezolvarea ecuațiilor logaritmice nu dau doar un răspuns la problema, are ca rezultat o explicație detaliată soluție. și anume Acesta arată procesul de a obține un răspuns.

Acesta poate fi util pentru elevii din clasele superioare ale școlilor secundare în curs de pregătire pentru teste și examene de verificare a cunoștințelor, înainte de examen, părinții să monitorizeze soluțiile la mai multe probleme de matematica si algebra. Sau poate că sunt prea scumpe pentru a angaja un tutore sau de a cumpăra cărți noi? Sau vrei doar cât mai repede posibil pentru a face temele la matematică sau algebră? În acest caz, puteți profita de asemenea programele noastre cu soluții detaliate.

Astfel, puteți efectua propria lor de formare și / sau educația fraților lor mai mici sau surori, la același nivel de educație în domeniul sarcinilor crește.

log (b) sau log (e, b) - logaritmului natural al b
log (10, b) - logaritmul zecimal al b
log (a, b) - logaritmul b la baza A

pentru că dispus pentru a rezolva problema foarte mult, cererea dumneavoastră este în coada de așteptare.
După câteva secunde, soluția va apărea mai jos.
Vă rugăm să așteptați o secundă. Nu vreau să aștept!

Aceste soluții sunt create și stocate de către utilizatori pe serverul nostru
folosind acest calculator on-line.

Funcția logaritmică. logaritmi

Problema 1. Găsiți rădăcina pozitivă a ecuației x 4 = 81
Prin definiție, avem aritmetică rădăcină \ (x = \ sqrt [4] = 3 \)

Problema 2. Să se rezolve ecuația 81 x = 3
Noi scriem ecuația după cum urmează: x = 3 4. 3 unde x = 4

In sarcina 1 nu este cunoscută măsura de bază, și o problemă de 2 - exponent. 2 Metoda de rezolvare a problemei a fost că partea stângă și dreaptă a ecuației poate fi reprezentată ca un grad cu aceeași bază 3. Dar, de exemplu, ecuația 3 x = 80 în acest fel nu este posibil să o rezolve. Cu toate acestea, această ecuație are o rădăcină. Pentru a putea rezolva aceste ecuații, introducem conceptul de logaritmul numărului.
Ecuația a x = b, unde a> 0, \ (a \ neq 1 \), b> 0, are o rădăcină unică. Această rădăcină se numește logaritmul b nici o bază și un b desemnat Loga
De exemplu, rădăcina ecuației 81 x = 3 este numărul 4, adică, log3 4 = 81.

Definiția. Logaritmul unui număr pozitiv în baza b-o, în cazul în care un> 0, \ (o neq 1 \ \) este numit exponent, pe care doriți să ridice numărul de a, pentru a obține b

log2 8 = 3, deoarece 2 3 = 8

log7 7 = 1, din 7 = 7 1

Determinarea logaritmului poate fi scris ca:

Această ecuație este valabilă pentru b> 0, b> 0 \ (a \ neq 1 \). Acesta este de obicei menționată ca identitatea logaritmică principală.

Acțiunea de a găsi logaritmul numărului numit logaritmi.
Acțiunea de determinare a numărului de logaritm sale se numește potențarea.

Calculați log64 128
Fie x = log64 128. Prin definiție, 64 logaritm x = 128. De la 64 = 2 6. 128 = 2 7. 2 = 6x 7. 2 de la 6x = 7, x = 7/6.
Raspuns log64 128 = 7/6

Calculați \ (^ 3 \)
Folosind proprietățile și gradul de identitate logaritmic de bază, vom găsi

Rezolva ecuația log3 (1-x) = 2
Prin logaritm definiție luna martie 2 = 1 - x, unde x = -8

Proprietățile logaritmi

Când transformările expresiilor ce conțin logaritmi, în calcule și ecuațiile pentru rezolvarea diferite proprietăți sunt adesea folosite logaritmi. Luați în considerare cele mai importante.

Să presupunem că un> 0 \ (a \ neq 1 \), b> 0, c> 0, r - orice număr real. Apoi, următoarea formulă:

2) \ (\ log_a \ frac = \ log_a b - \ log_a c \)

logaritmi zecimale și naturale

Pentru logaritmilor numerelor trase tabele speciale (tabele de logaritmi). Logaritmi, calculat de calculator. În acest lucru și în celălalt caz sunt doar logaritmi zecimali sau naturale.

Definiția. logaritmul zecimal al numărului se numește logaritmul numărului de bază 10 și scrise
lg b în schimb log10 b

Definiția. Logaritmul natural al numărului numit logaritmul numărului la serviciul e de bază, în cazul în care e - număr irațional, aproximativ egal cu 2,7. Când această scriere ln b în loc Loge b

Numărul Iraționale e joacă un rol important în matematică și aplicațiile sale. Numărul e poate fi reprezentat ca suma:
$$ e = 1 + \ frac + \ frac + \ frac + \ dots + \ frac + \ puncte $$

$$ e \ cca 2,7182818284 $$

Se pare că este suficient doar să cunoască valorile zecimale sau doar logaritmii naturale de numere pentru a găsi logaritmilor numerelor din orice motiv.
Pentru acest scop înlocuirea formulei de bază logaritm:

unde b> 0, a> 0, \ (a neq 1 \ \), c> 0, \ (c \ neq 1 \)

Consecințele bazei logaritm formulei de înlocuire.
Dacă c = 10 și c = e obținut prin formula de tranziție în zecimal logaritmi și naturale:
$$ \ log_a b = \ frac. \; \; \ Log_a b = \ frac $$

Funcția logaritmică, proprietățile sale și programul

În matematică și aplicațiile sale funcționale logaritmică comune
y = x LOGA
și în care - numărul predeterminat, a> 0, \ (a \ neq 1 \)

Funcția logaritmică are următoarele proprietăți:
1) Domeniul funcției logaritmice - mulțimea tuturor numerelor întregi pozitive.

2) Valorile de referință ale funcției logaritmice - mulțimea tuturor numerelor reale.

3) Funcția logaritmică nu este limitată.

4) Funcția logaritmică y = x este LOGA la creșterea intervalului \ ((0; + \ infty) \), în cazul în care a> 1,
și în scădere dacă 0 1, atunci funcția y = x LOGA ia valori pozitive pentru x> 1,
negativ pentru 0 1.

axa Oy este asimptota verticală a graficului y = x LOGA

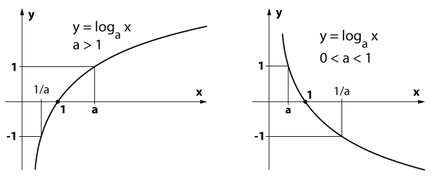
Rețineți că orice grafic al funcției logaritmice y = x LOGA trece prin punctul (-1; 0).
In rezolvarea ecuațiilor utilizate adesea teorema următoare:

Logaritmică Funcția y = x și LOGA funcția exponențială y = a x. unde a> 0, \ (a \ neq 1 \) sunt reciproc invers.

ecuații logaritmice

Rezolva log2 ecuația (x + 1) + log2 (x + 3) = 3
Să presupunem că x - este un număr la care egalitatea este adevărată, adică, x - rădăcina ecuației. Apoi, prin proprietatea logaritmului egalității
log2 ((x + 1) (x + 3)) = 3
Din această ecuație pentru a determina logaritmului obținem
(X + 1) (x + 3) = 8
x 2 + 3 + 4 = 8, adică, x 2 + 4x - 5 = 0, x1 = 1, x2 = -5
Deoarece ecuația de gradul doi este o consecință a ecuației inițiale, este necesar să se verifice.
Verificați dacă numerele 1 -5 și rădăcinile ecuației originale.
Substituind partea stângă a ecuației inițiale x = 1, obținem
log2 (1 + 1) + log2 (1 + 3) = log2 2 + log2 = 1 + 4 2 = 3, adică x = 1 - rădăcina ecuației.
Când x = -5 + 1 număr x + 3 și x este negativ, și, prin urmare, partea stângă a ecuației nu are sens, adică = -5 x nu este o rădăcină a acestei ecuații.
Răspunsul este x = 1

Lg rezolva ecuația (2x 2 - 4x + 12) = lg x + lg (x + 3)
Prin proprietatea logaritmilor
lg (2x 2 - 4x + 12) = lg (x 2 + 3x)
de unde
2 2x - 4x + 12 = x 2 + 3x
x 2 - 7x + 12 = 0
x1 = 3, x2 = 4
Testarea arată că cele două valori ale lui x sunt rădăcinile ecuației originale.
x1 Response = 3, x2 = 4

Rezolva log4 ecuația (2x - 1) • log4 x = 2 log4 (2x - 1)
Să transformăm această ecuație:
log4 (2x - 1) • log4 x - 2 log4 (2x - 1) = 0
log4 (2x - 1) • (log4 x - 2) = 0
Asimilarea fiecare factor în partea stângă a ecuației la zero, obținem:
1) log4 (2 - 1) = 0, unde 2 - 1 = 1, x1 = 1
2) log4 x2 = 0 unde log4 = 2, x2 = 16
Testarea arată că cele două valori ale lui x sunt rădăcinile ecuației originale.
Răspuns x1 = 1, x2 = 16

Cărți (cărți) Cărți (altele), rezumate examen și OGE teste de jocuri online, puzzle-uri Trasarea de dicționar de școli catalog argotic tineret România Catalog SSUZov România Catalog România universităților Probleme la găsirea GCD și polinomiale LCM Simplificarea (multiplicarea polinomul) Diviziunea polinom printr-un calcul coloană polinom fracțiunile numerice Rezolvarea problemelor în procente numere complexe: sumă, diferență, produs și sisteme Quotient 2 ecuații liniare cu două variabile Soluția ecuației pătratice bold dvuch pătrat Lena și factoring pătratice Inegalități decizie polinomiale decizie inegalități diagrame funcție pătratică sistem Graphing funcție fracționată liniară rezolva aritmetică și geometrică trigonometric decizie progresii, exponențiale, ecuații logaritmice Calculul limitelor, tangente, integrale primitive triunghiuri de soluție Calculele acțiunilor derivate cu vectori Calcule linia de acțiune și planul zonei de forme geometrice forme geometrice pe perimetrul em geometric suprafață forme de forme geometrice
Designer situații de conducere
Vremea - Stiri - Horoscop
Programul MathSolution.ru pe Google Play