Calculator online - pentru a calcula definită integral (zona curbată a trapezului)

Acest calculator matematic online pentru a vă ajuta să calculeze integrala definit (zona trapezului curbilinie). Program pentru a calcula o integrală definită (aria unui trapez curbilinie) nu numai că dă răspunsul la problema, are ca rezultat o explicație detaliată soluție. și anume Acesta arată procesul de integrare a funcției.

Acesta poate fi util pentru elevii din clasele superioare ale școlilor secundare în curs de pregătire pentru teste și examene de verificare a cunoștințelor, înainte de examen, părinții să monitorizeze soluțiile la mai multe probleme de matematica si algebra. Sau poate că sunt prea scumpe pentru a angaja un tutore sau de a cumpăra cărți noi? Sau vrei doar cât mai repede posibil pentru a face temele la matematică sau algebră? În acest caz, puteți profita de asemenea programele noastre cu soluții detaliate.

Astfel, puteți efectua propria lor de formare și / sau educația fraților lor mai mici sau surori, la același nivel de educație în domeniul sarcinilor crește.

pentru că dispus pentru a rezolva problema foarte mult, cererea dumneavoastră este în coada de așteptare.
După câteva secunde, soluția va apărea mai jos.
Vă rugăm să așteptați o secundă. Nu vreau să aștept!

Aceste soluții sunt create și stocate de către utilizatori pe serverul nostru
folosind acest calculator on-line.

Certe de integrală.
Probleme care conduc la conceptul de definit integralei

Sarcina 1 (pentru calcularea ariei unui trapez curbilinie).

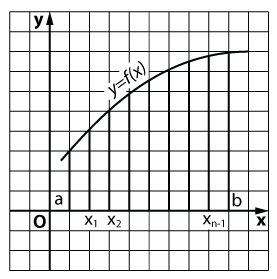
Sistemul xOy figura dat (a se vedea. Figura) delimitat de axa x, liniile drepte x = a, x = b coordonate carteziene (a

Conceptul integrala definită

Dăm o descriere matematică a modelului care a fost construit în trei sarcini avute în vedere pentru o funcție y = f (x), continuă (dar nu neapărat non-negativ, așa cum sa presupus în problemele considerate) în intervalul [a; b]:
1) împărțit intervalul [a; b] pentru n părți egale;
2) este suma

3) se calculează

În cursul analizei matematice a demonstrat că această limită în cazul unei funcții continue (sau piese înțelept continuă) există. Se numește integrala definită a unei funcții y = f (x) pe intervalul [a; b] și se notează după cum urmează:







Numerele a și b se numesc limitele de integrare (respectiv, inferior și superior).

Să ne întoarcem la problemele discutate mai sus. Determinarea suprafeței date în Problema 1 poate fi acum rescrisă după cum urmează:

Aici S - zona unui trapez curbilinie prezentat în figura de mai sus. Acesta este sensul geometric al integralei definit.

Determinarea deplasării s a unui punct se deplasează într-o linie dreaptă la o viteză de v = v (t), pentru un interval de timp de la t = a la t = b, dată în Problema 2 poate fi rescrisă ca:

Formula lui Newton - Leibniz

Pentru a începe să răspundă la întrebarea: Care este relația dintre bine definit integral si primitiv?

Răspunsul poate fi găsit în sarcină 2. Pe de o parte, deplasarea s a unui punct se deplasează într-o linie dreaptă la o viteză de v = v (t), intervalul de timp de la t = a și t = b și se calculează conform formulei

Pe de altă parte, punctul de coordonate se mișcă primitiv pentru viteza - denote s sale (t); înseamnă deplasarea exprimată prin formula s s = s (b) - s (a). Ca rezultat, obținem:

în cazul în care s (t) - primitive pentru v (t).

În cursul analizei matematice a demonstrat următoarea teoremă.
Teorema. Dacă funcția y = f (x) este continua pe intervalul [a; b], atunci formula următoare

unde F (x) - primitivă f (x).

Formula de mai sus este de obicei numita formula Newton - Leibniz după fizicianul englez Isaaka Nyutona (1643-1727) și filozoful german Gottfried Leibniz (1646- 1716), a primit în mod independent și practic simultan.

În practică, în loc de a scrie F (b) - intrarea F (a) se utilizează (este numit uneori substituție dublă), și în consecință, rescrie formula Newton - Leibniz în forma:

Calcularea integrală definită, în primul rând găsi se realizează o substituție primitivă, apoi dublu.

Pe baza formulei lui Newton - Leibniz, este posibil să se obțină două proprietăți ale definit integralei.

Proprietatea 1. Integrala suma funcțiilor este egală cu suma integralelor:

Proprietatea 2. Un factor constant poate fi luată în afara semnului integrală:

Calcularea zonelor de figuri plane prin intermediul integralele definite

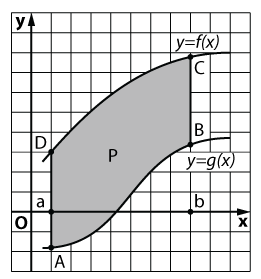
Utilizarea integrală poate fi suprafață calculată nu este doar trapez curbilinie, dar avionul cifrele o formă mai complicată, cum ar fi cea prezentată în fig. Figura F delimitată de liniile x = a și x = b și diagrame funcție continuă y = f (x), y = g (x), în care intervalul [a; b] inegalitate. Pentru a calcula suprafața S a figurii, vom proceda după cum urmează:

Deci, forma zona S, mărginită de linii x = a și x = b și funcția grafică y = f (x), y = g (x), continuă pe intervalul [a; b] și astfel încât pentru orice x intervalul [a; b] inegalitatea se calculează cu formula:

Tabelul integralelor nedefinite () a anumitor primitive funcții

$$ \ int 0 \ cdot dx = C $$

$$ \ int 1 \ cdot dx = x + C $$