Ce este ERF
3.3.Temperaturnoe câmp continuu punct staționar sursă-ni-ka într-un mediu infinit. Funcția de eroare gauss (erf (x)).
În cazul în care punctul de-ke cu coordonatele x“. y“. z „în intervalul de timp de la t“ = 0 până la t „= t ra-bot sursă de căldură putere W, domeniul de temperatură al IP-point-audio-ka, așa cum este definit mai sus, mo-Jette fi găsit prin integrarea soluția fundamentală a t“ de la 0 la t (adică, de la pornire până la oprire). Localizați originea coordonatelor, până la punctul în care sursa de la TEP. Apoi, x '= y' = z „= 0, iar formula pentru temperatura devine:
Noi face parte integrantă (3.3.1) modificarea variabilelor: r2 / [4a (t - t „)] = 2. Apoi: (t - t ') 3/2 = r3 / (8a3 / 23), dt' = r2d / (2a3). limitele integrării: t „= 0
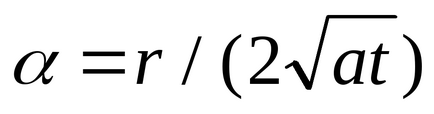
Prima integrală în paranteze, este cunoscut de un curs de matematici superioare:
iar a doua integrală în ceea ce privește funcțiile elementare nu pot fi exprimate, și definește o distracție-to-TION speciale, care se numește erorile funcției Gauss. sau integralei de probabilitate. sau fun-to-chi-ea erfektum:
(Citiți "erfektum" sau abrevierea "ORF"). Prin această funcție soluția exprimată de problemele-set mulți, în teoria conducție a căldurii, precum și în alte domenii ale fizicii joacă un rol important.
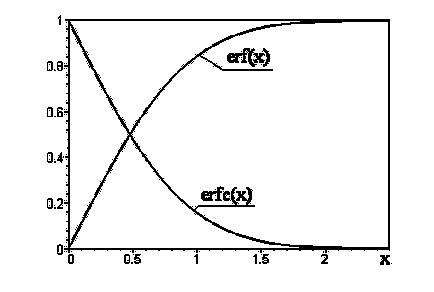
Din definiția (3.3.3) care erf (0) = 0, și erf () = 1, adică erf (x) - este o funcție-dar-Cant tonalitate dar în creștere pentru a vedea un roi izo-in Figura 3.3 prin lipire. Funcția erf (x) ta-bu-li - po-wang și sale ZNA-cheniya plumb-time camping în cărți de referință Lich-guvernamentale; Tabelul 3.1 la Insula de noi câteva valori ale acestei funcții. Bib-li-o-te-Kah nu-la-toryh limbaje de programare-TION sunt de o-tiile în cadrul pro-gram pentru tine functia ne-Num-MENT ERF (x). Dacă vă pregătiți pro - gram, nu avem, ERF funcția (x) poate fi tu-Num-turnat folosind o serie de putere. o dată-lo-tensiune-TION a acestei funcții în număr-pen-ste clorhidric, care este de obicei conținut în matematică-Ches-CAL spra-Voch-tori, având un form- "ing Mill-cadou-t-":
E
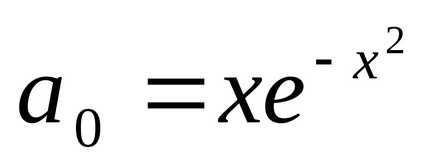
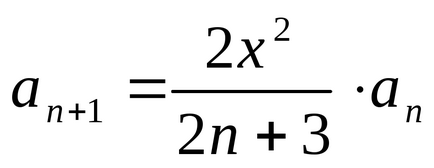
acest număr ușor twist-program de vychisleniyaerf (x) pe limba lu-BOM programul-E TION și da este un programat micro-Kal-ku la torus. Însumare necesară pre-margine-Schat, co-GDS prin adaugarea Oche-ed-dar-lea termen al unei sume de opriri me-nyatsya (pentru a fi pre-Stig-nu-ta "precizie ma-pneu-evaluate").
Dacă este necesară o mai mare precizie, puteți utiliza cote aproximative-catâr:
Formula (3.3.6) prezintă valorile, eroarea absolută care nu mai mult de 6.310 -3. și eroarea nu mai mult de 0,71% otno-B Tel-evaluate.
Uneori, în intervalul negativ este necesară pentru a determina erf (x) x. Formula (3.3.3), este evident că erf (-x) = - erf (x).
Rețineți că, deși funcția ERF (x) nu este un „elementar“, din punct de vedere TION a proprietăților și a metodelor sale pe care-Num-ment este mai ușor decât majoritatea funcțiilor „de bază“, cum ar fi trigonometrie.
Deoarece funcția ERF (x) este mai multe funcții legate de comune pentru încălzirea-fi-communication-CHES-cal probleme. Acest lucru este în primul rând ve-ro-Yat-Ness o integrală suplimentară:
care apare atât de des încât o notație specială folosită pentru ea: ERFC (x) (prescurtat pentru a citi „erfik“). Forma acestei funcții este de asemenea prezentată în Figura 3.3.
Destul de des, ERF funcția (x) trebuie să fie diferențiate și în cele care-grirovat. Din op-re-de-ment (3.3.3) rezultă că
și integrala ERFC (x) (notat ca ierfc (x)) este egal cu:
Revenind la Formula (3.3.2). Notând că ca = . putem scrie această formulă ca:
Când t valoare funcție
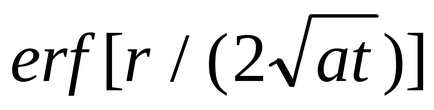
Tabelul 3.1. Unele valori ale ERF funcției (x).