Ce este o funcție monotonă de 1

1.3.5. funcții monotone

f (x) funcția este numită creșterea diferenței D. Dacă, pentru orice numere întregi x 1 și x 2 din decalajul D, astfel încât x 1

f (x) funcția este numită reducerea decalajului D. Dacă pentru numere întregi x 1 și x 2 din decalajul D, astfel încât x 1 f (x 2).

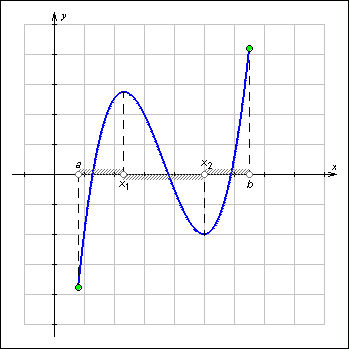
Intervale de creștere și funcția de scădere

În graficul prezentat în figura funcției y = f (x). crește la fiecare din intervalele [a; x 1) și (x 2; b] și scade diferența (x 1, x 2). De notat că creșterile funcționale în fiecare din intervalele [a; x 1) și (x 2, b], dar nu în combinație. lacune

În cazul în care funcția este în creștere sau în scădere pe unele interval de timp, atunci se numește monotonă pe acest interval.

Rețineți că, dacă f - o funcție monotonă a intervalului D (f (x)). ecuația f (x) = const poate avea mai mult de o rădăcină în acest interval.

Într-adevăr, dacă x 1

Enumerăm proprietățile funcțiilor monotone (se presupune că toate funcțiile definite pe un anumit interval D).

• Suma de mai multe funcții în creștere este o funcție crescătoare.
• Lucrare funcția de creștere nenegativ este o funcție crescătoare.
• Dacă funcția f este mărită, atunci funcțiile cf (c> 0) și f + c, de asemenea, crește, iar funcția cf (c <0) убывает. Здесь c – некоторая константа.
• În cazul în care crește f și își păstrează semnul său, funcția 1 / f scade.
• În cazul în care funcția f este în creștere și este non-negativ, atunci în cazul în care. De asemenea, crește.
• Dacă crește f și n - impar, atunci f n crește.
• Compoziția g (f (x)) creșterea funcțiilor f și g, de asemenea, crește.

Declarații similare pot fi formulate pentru funcția descrescătoare.

Modelul 1.9. proprietăți ale funcției

un punct se numește un maxim al funcției f. în cazul în care există un ε-vecinătate a unui. că inegalitatea f (a) ≥ f (x) pentru fiecare x din acest cartier.

un punct numit punctul de minim al funcției f. în cazul în care există un ε-vecinătate a unui. că pentru orice x din acest complex inegalitatea f (a) ≤ f (x).

Momentul în care maximul sau minimul unei funcții, numită punctele extremum.

Punctul de extremelor este o schimbare a caracterului de monotonie. Deci, la stânga punctului funcției extremelor poate crește, și dreptul - să scadă. Prin definiție, punctul extremale ar trebui să fie un punct din interiorul domeniului.

Dacă pentru orice (x ≠ a) inegalitatea f (x) ≤ f (a), atunci punctul este numit un punct de valori maxime ale setului D.

Dacă pentru orice (x ≠ b) inegalitatea f (x)> f (b) litera b este un punct de valoare mai mică pe setul D.

cele mai mari sau mai mici valori ale unui punct poate fi funcția extremelor, dar nu neapărat este.

Cel mai înalt punct (cea mai mică), valoarea funcției continuă la intervalul care urmează să fie găsit printre extremele acestei funcții și valorile sale la punctele finale.