Proprietățile înmulțirii numerelor naturale

Pornind de la prezentarea generală a înmulțirii numerelor naturale. se poate observa o serie de rezultate, specifice acestei activități. Aceste rezultate sunt numite proprietăți inerente de multiplicare a numerelor naturale. În acest articol vom arăta câteva exemple de proprietățile de bază ale înmulțirii numerelor naturale și să le scrie cu litere.

Navigare în pagină.

Comutativitate de multiplicare a numerelor naturale.

Înmulțirea a două numere întregi are proprietatea comutative. Aici formularea proprietăților: produsul a două numere întregi nu se schimbă atunci când multiplicatorii permutare locuri. Cu litere ale Comutativitate de multiplicare poate fi scris ca: a · b = b · o. unde a și b pot fi orice numere naturale (dacă este necesar, a se vedea articolul de expresie literală).

Luați în considerare exemplul care confirmă validitatea Comutativitate de multiplicare a două numere naturale. Bazat pe sensul de multiplicare a două numere naturale. Se calculează produsul dintre numerele 2 și 6, precum și produsul dintre numerele 6 și 2, și să verifice că rezultatele de multiplicare. Produsul a numerelor 6 și 2 egal cu suma 6 + 6. din tabelul de adăugare este 6 + 6 = 12. Un produs al numerelor 2 și 6 este suma 2 + 2 + 2 + 2 + 2 + 2. care este egală cu 12 (dacă este necesar, a se vedea materialul de articol și adăugarea a încă trei numere). Prin urmare, 6 x 2 x 2 = 6.

Este o diagramă care ilustrează Comutativitate de multiplicare a două numere naturale.

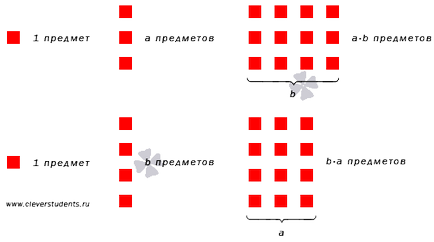
asociativitate de multiplicare a numerelor naturale.

Supranumit de asociativitate de multiplicare a numerelor naturale: Înmulțiți acest număr cu acest produs de două numere - este aceeași cu cea de a multiplica acest număr de primul factor, iar rezultatul înmulțit cu al doilea factor. Adică, o · (b · c) = (a · b) · c. în cazul în care un. b și c pot fi orice numere naturale (în paranteze sunt incluse valorile de expresie sunt calculate în primul rând).

Aici este un exemplu pentru a confirma proprietățile asociative ale înmulțirea numerelor naturale. Calculati produsul de 4 · (3 · 2). În sensul înmulțirii au 3 · 2 = 3 + 3 = 6. apoi 4 + (3 x 2) = 4 x = 4 + 6 4 + 4 + 4 + 4 + 4 = 24. Acum efectuați multiplicare (4 * 3) · 2. Deoarece 4 · = 4 + 3 4 + 4 = 12. apoi (3 · 4) = 12 · 2 · 12 + 2 = 12 = 24. Astfel, egalitatea 4 · (3 · 2) = (3 · 4) · 2. confirmând valabilitatea proprietății în cauză.

Afișăm desen care ilustrează proprietatea asociativă de multiplicare a numerelor naturale.

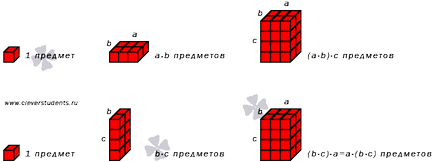
Pentru a încheia această secțiune observăm că proprietatea asociativă de multiplicare se poate defini în mod unic o multiplicare a trei sau mai multe numere întregi.

proprietate distributivă de multiplicare de peste plus.

Următoarea proprietate se leagă și de multiplicare plus. Acesta este formulat după cum urmează: multiplica această sumă a două numere de pe acest număr - este același lucru ca și produsul pliat al primului termen și numărul dat la produsul de al doilea termen și numărul. Această așa-numita proprietate distributivă de multiplicare de peste plus.

Iată un exemplu care confirmă proprietatea distributiv de multiplicare a numerelor naturale. Noi verifica validitatea ecuației (3 + 4) = 2 · 3 · 2 + 4 · 2. Avem (3 + 4) * 2 = 7 x = 7 + 2 7 = 14. și 3 · 2 + 4 · 2 = (3 + 3) + (4 + 4) = 6 + 8 = 14. prin urmare, ecuația (3 + 4) = 2 · 3 · 2 + 4 · 2 este adevărat.

Pretindem model care corespunde proprietății distributiv de multiplicare de peste plus.

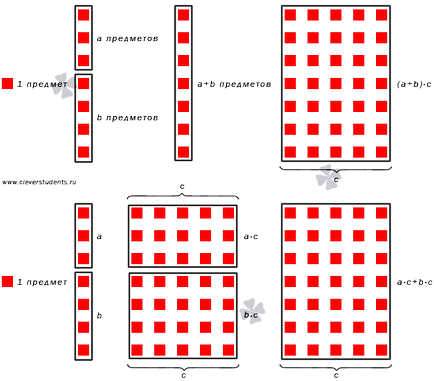
proprietate distributivă de multiplicare în ceea ce privește scăderea.

Multiplicarea și scăderea numerelor naturale sunt asociate proprietății distributiv. Consoană formularea sa: înmulțească această diferență de două numere naturale date pentru un număr natural - este ca cea a produsului și numărul redus al Scăzător și scade produsul dintre numărul.

Folosirea scrisorilor de proprietate distributivă de multiplicare în ceea ce privește scăderea poate fi scris ca (a-b) · c = a · c-b · c. în cazul în care un. b și c - sunt numere naturale. În virtutea proprietății comutative de multiplicare, formula formează, de asemenea, o · (b-c) = a · b-o · c.

Verificați validitatea proprietăților de distribuție ale înmulțirii cu privire la exemplul de scădere. Să ne arată că egalitatea de 3 * (4-2) = 3 · 4-3 · 2. Deoarece 4-2 = 2 (dacă este necesar, a se vedea secțiunea de scădere teorie folosind tabelul de adăugare), apoi produsul 3 · (4-2) este egal cu produsul de 3 · 2. și 3 x 2 = 3 + 3 = 6. Acum, să ne calculeze diferența 3 · 4-3 · 2. Au 3 · 4-3 · 2 = (3 + 3 + 3 + 3) - (3 + 3) = 12-6 = 6. Astfel, ecuația 3 * (4-2) = 3 · 4-3 · 2 dreapta.

unitate de proprietate de înmulțire cu un număr natural.

Următoarea proprietate este asociat cu unitatea de multiplicare și un număr natural. În sensul înmulțirii, produsul a unității și a numărul natural n este egal cu suma n termeni, fiecare dintre care este egal cu unu. În consecință ,.

De exemplu, produsul dintre numerele 1 și 37 este egal cu 37; înmulțirea rezultatului de 1 și 1004 este numărul de 1004.

La rândul său, produsul de n · 1 este lipsită de sens (în sensul înmulțirii acestei lucrări este suma unui termen egal cu numărul n. Adaosul dar am fost determinate pentru doi sau mai mulți termeni). Pentru a rămâne adevărat Comutativitate de multiplicare, presupunem că adevărata egalitate n · 1 = n.

De exemplu, produsul este egal cu 298 și 1 298. și dacă înmulțit cu 1. 71 obținem 71.

Astfel, produsul a două numere întregi pozitive, dintre care unul este egal cu un egal cu un alt număr. Ultima afirmație este proprietățile de formulare ale unităților de multiplicare și un număr natural. Folosind această proprietate de scrisori de multiplicare scrise ca: 1 · n = n · 1 = n. unde n - orice număr întreg.

proprietatea Multiplicarea zero la un număr întreg.

Deși zero nu este un număr natural, dar încă proprietatea de multiplicare de la zero și un număr întreg pozitiv, vom acoperi în acest articol. Acest lucru se datorează faptului că această proprietate este utilizat în multiplicarea coloanei numere naturale.

Dacă ne menținem la sensul de multiplicare, produsul de la 0 · n. unde n - un număr natural arbitrar mai mare decât unu, n este suma termenilor, fiecare dintre acestea fiind zero. Astfel. Proprietățile adăugarea ne permit să afirmăm că această din urmă sumă este egală cu zero.

Pentru a păstra validitatea proprietăților de multiplicare a numerelor naturale pe unitatea, pe care le-am discutat în paragraful precedent, vor fi luate în considerare corect următoarea ecuație 0 · 1 = 0.

Astfel, pentru orice număr natural n, egalitatea 0 · n = 0.

Pentru a rămâne adevărat Comutativitate de multiplicare, de asemenea, să ia egalitatea n · 0 = 0 pentru orice număr natural n.

Astfel, produsul de la zero și un număr întreg pozitiv egal cu zero. adică 0 · n = 0 și n · 0 = 0. unde n - număr natural. Ultima afirmație este o declarație a proprietăților de înmulțire a numerelor naturale și zero.

În concluzie, prezentăm două exemple legate pentru a înțelege această proprietate punct de multiplicare. Produsul a numerelor 45 și 0 este zero. 0 Dacă se înmulțește cu 45 970. Faptul, de asemenea, vom ajunge la zero.

Acum puteți începe în condiții de siguranță a învăța regulile prin care a avut loc inmultirea numerelor naturale.

• Matematica. Orice manuale pentru 1, 2, 3, 4 clase de instituții de învățământ.
• Matematica. Orice tutoriale pentru 5 clase de instituții de învățământ.